✏️ 완전 탐색이란?
주어진 수를 통해 가능한 경우의 수를 모두 나열하여 원하는 답을 찾아내는 기법.
- Brute-Force 기법
- 순열
- 재귀함수
- 비트마스크
- DFS, BFS
순열 재귀 방식
순열은 서로 다른 N개의 원소를 가지는 어떠한 집합에서 중복없이 순서에 상관있게 R개의 원소를 선택하거나 나열하는 것
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
function permutations(arr: number[]) {
const result: number[][] = [];
/**
* 재귀적으로 순열을 생성하는 내부 함수
* @param currentPermutation 현재까지 만든 순열
* @param remainingElements 아직 사용하지 않은 원소들
* @returns 모든 순열 반환
*/
function generate(currentPermutation: number[], remainingElements: number[]) {
// 남은 원소가 없으면, 하나의 순열이 완성된 것
if (remainingElements.length === 0) {
result.push(currentPermutation); // 결과에 추가
return;
}
// 남은 원소들 각각에 대해 반복
for (let i = 0; i < remainingElements.length; i++) {
// i번째 원소를 선택
const choose = remainingElements[i];
// 선택한 원소를 현재 순열에 추가 후 다음 순열 생성
const nextPermutation = [...currentPermutation, choose];
// 선택한 원소를 제외한 나머지로 다음 순열 생성
const nextRemaining = remainingElements.filter((_, index) => i !== index);
// 재귀 호출
generate(nextPermutation, nextRemaining);
}
}
// 초기값: 빈 순열, 전체 배열
generate([], arr);
return result;
}
permutations([1, 2, 3]);
[ [ 1, 2, 3 ], [ 1, 3, 2 ], [ 2, 1, 3 ], [ 2, 3, 1 ], [ 3, 1, 2 ], [ 3, 2, 1 ] ]
1
응용 문제 - 피로도
플레이어가 현재 피로도 k를 가지고 던전들을 최대한 많이 탐험하는 것
- 각 던전의 두 가지 정보
- 최소 필요 피로도: 이 던전에 진입하기 위해 필요한 최소한의 피로도
- 소모 피로도: 이 던전을 탐험하고 나면 줄어드는 피로도
- 제한 사항
- 총 던전의 개수는 최대 8개
- 피로도 및 던전 관련 수치는 자연수이며 특정 범위 내에 있음
주어진 k와 각 던전의 정보를 바탕으로 유저가 탐험할 수 있는 최대 던전 탐험 수를 반환하는 함수 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
const dungeons = [
[80, 20],
[50, 40],
[30, 10],
];
const k = 80;
// result: 3
/**
* 주어진 순서대로 던전을 탐험하며, 탐험 가능한 던전 수를 반환
* @param games 던전 배열 (방문 순서대로)
* @param k 시작 피로도
* @returns 탐험한 던전 수
*/
function calculation(games: number[][], k: number) {
let fatigue = k; // 현재 남은 피로도
let rotation = 0; // 탐험한 던전 수
for (let i = 0; i < games.length; i++) {
const minimumFatigue = games[i][0]; // 최소 필요 피로도
const exhaustionFatigue = games[i][1]; // 소모 피로도
// 피로도가 부족하면 더 이상 탐험 불가
if (fatigue < minimumFatigue) {
break;
}
fatigue -= exhaustionFatigue; // 피로도 소모
rotation++; // 탐험한 던전 수 증가
}
return rotation;
}
/**
* 모든 던전 방문 순서(순열)를 만들어 각 경우마다 탐험 가능한 던전 수를 계산
* @param array 던전 배열
* @param k 시작 피로도
* @returns 각 순열별 탐험한 던전 수 배열
*/
function permutation(array: number[][], k: number) {
const result: number[] = [];
// 재귀적으로 순열 생성
function generate(current: number[][], remaining: number[][]) {
// 남은 던전이 없으면, 현재 순서로 탐험 가능한 던전 수 계산
if (remaining.length === 0) {
result.push(calculation(current, k));
return;
}
// 남은 던전 각각에 대해 순서 선택
for (let i = 0; i < remaining.length; i++) {
const choose = remaining[i]; // i번째 던전 선택
const nextPermutation = [...current, choose]; // 현재 순서에 추가
const nextRemaining = remaining.filter((_, index) => i !== index); // 선택한 던전 제외
generate(nextPermutation, nextRemaining); // 재귀 호출
}
}
generate([], array); // 초기값: 빈 순서, 전체 던전
return result;
}
/**
* 최대한 많은 던전을 탐험할 수 있는 경우의 수를 구하는 함수
* @param k 시작 피로도
* @param dungeons 던전 배열
* @returns 탐험 가능한 최대 던전 수
*/
function solution(k: number, dungeons: number[][]) {
const result = permutation(dungeons, k); // 모든 순열별 결과
return result.sort((a, b) => b - a)[0]; // 최대값 반환
}
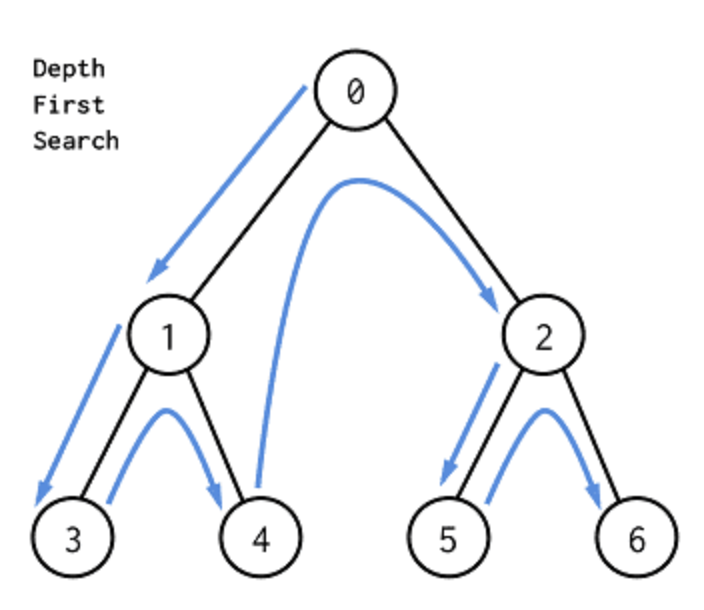
DFS
DFS는 그래프나 트리를 탐색하는 알고리즘 중 하나로 한 방향으로 갈 수 있는 한 최대한 깊이 들어간 다음 더 이상 갈 곳이 없으면 뒤로 돌아와(백트래킹) 다른 경로를 탐색하는 방식
- 시작 노드 선택: 탐색을 시작할 노드(정점)를 하나 선택
- 방문 표시: 현재 노드를 ‘방문’했다고 표시 (중복 방문을 막기 위함)
- 깊이 우선 탐색: 현재 노드와 연결된 방문하지 않은 노드가 있다면 그 노드로 이동하여 다시 2단계부터 즉, 최대한 깊이 탐색
- 백트래킹: 더 이상 방문할 수 있는 노드가 없으면 이전 노드로 돌아와서(백트래킹) 다른 경로가 있는지 확인
- 모든 노드 방문: 이 과정을 모든 노드를 방문할 때까지 반복
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
type DFSGraph = Record<string, string[]>;
const dfs_graph: DFSGraph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "E", "F"],
D: ["B"],
E: ["C"],
F: ["C"],
};
/**
* 깊이 우선 탐색(DFS) 함수
* @param tree 그래프 (인접 리스트 형태)
* @param root 시작 노드
* @returns 방문한 모든 노드들의 Set
*/
function dfs(tree: DFSGraph, root: string) {
// 방문한 노드들을 저장할 Set (중복 방문 방지)
const result = new Set();
/**
* 재귀적으로 노드를 탐색하는 내부 함수
* @param targetNode 현재 탐색할 노드
*/
function generate(targetNode: string) {
// 현재 노드를 방문 처리
result.add(targetNode);
// 현재 노드의 모든 인접 노드들을 순회
for (let i = 0; i < tree[targetNode].length; i++) {
// 아직 방문하지 않은 노드라면 재귀적으로 탐색
if (!result.has(tree[targetNode][i])) {
generate(tree[targetNode][i]);
}
}
}
generate(root);
return result;
}
dfs(dfs_graph, "A");
응용문제 - 타겟 넘버
n개의 음이 아닌 정수들로 순서를 바꾸지 않고 적절히 더하거나 빼서 타겟 넘버를 만들려고 합니다.
예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있습니다.
1
2
3
4
5
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 예시 입력 데이터
const NUMBERS = [1, 1, 1, 1, 1]; // 주어진 숫자 배열
const TARGET = 3; // 만들어야 할 타겟 숫자
/**
* 주어진 숫자들을 더하거나 빼서 타겟 숫자를 만드는 방법의 수를 구하는 함수
* @param numbers 주어진 숫자 배열
* @param initNumber 초기값 (보통 0)
* @returns 타겟 숫자를 만드는 방법의 수
*/
function solution(numbers: number[], initNumber: number) {
let result = 0; // 타겟 숫자를 만드는 방법의 수
/**
* 재귀적으로 모든 경우의 수를 탐색하는 함수
* @param index 현재 처리할 숫자의 인덱스
* @param calculated 현재까지 계산된 값
*/
function explore(index: number, calculated: number) {
// 모든 숫자를 처리했을 때
if (index === numbers.length) {
// 계산된 값이 타겟과 같으면 결과 카운트 증가
if (calculated === TARGET) {
result++;
}
return;
}
// 현재 숫자를 더하는 경우
explore(index + 1, calculated + numbers[index]);
// 현재 숫자를 빼는 경우
explore(index + 1, calculated - numbers[index]);
}
// 초기값 0부터 탐색 시작
explore(0, initNumber);
return result;
}
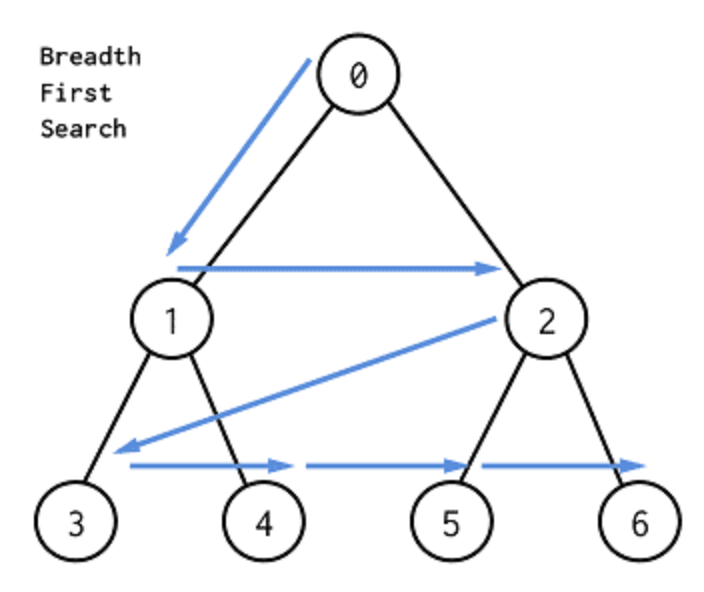
BFS
BFS는 그래프나 트리를 탐색하는 알고리즘 중 하나로 시작 노드에서 가까운 노드들을 먼저 탐색하고 점차 멀리 있는 노드들을 탐색하는 방식. 현재 노드에서 갈 수 있는 모든 인접 노드를 먼저 방문한 후 그 다음 레벨의 노드들을 방문하는 식으로 진행.
- 시작 노드 선택: 탐색을 시작할 노드(정점)를 하나 선택하고 이 노드를 Queue에 삽입
- 방문 표시: 큐에서 노드를 하나 꺼내어 ‘방문’했다고 표시 (중복 방문을 막기 위함)
- 인접 노드 탐색: 현재 꺼낸 노드와 연결된 방문하지 않은 모든 인접 노드들을 찾아 큐에 넣고 ‘방문 예정’ 상태로 표시
- 큐가 빌 때까지 반복: Queue가 빌 때까지 2단계와 3단계를 반복. Queue가 비면 모든 연결된 노드를 탐색한 것
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// BFS(너비 우선 탐색)를 위한 그래프 타입 정의
type BFSGraph = Record<string, string[]>;
const bfs_graph: BFSGraph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "E", "F"],
D: ["B"],
E: ["C"],
F: ["C"],
};
/**
* 너비 우선 탐색(BFS) 함수
* @param tree 그래프 (인접 리스트 형태)
* @param root 시작 노드
* @returns 방문한 모든 노드들의 Set
*/
function bfs(tree: BFSGraph, root: string) {
// 방문한 노드들을 저장할 Set (중복 방문 방지)
const result = new Set();
// BFS를 위한 큐
const queue: string[] = [root];
// 시작 노드를 방문 처리
result.add(root);
// 큐가 비어있을 때까지 반복
while (queue.length > 0) {
// 큐에서 노드를 하나 꺼냄 (가장 먼저 들어온 노드)
const current = queue.shift();
// 현재 노드의 모든 인접 노드들을 확인
for (let i = 0; i < tree[current].length; i++) {
const neighbor = tree[current][i];
// 아직 방문하지 않은 노드라면
if (!result.has(neighbor)) {
// 큐에 추가하고 방문 처리
queue.push(neighbor);
result.add(neighbor);
}
}
}
return result;
}
